第三章 知识大盘点
高考数学知识网络图
1.集合与简易逻辑
2.函数
3.数列
4.三角函数
(1)三角函数的图象和性质
| |
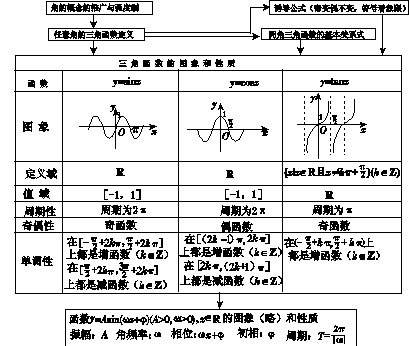
(2)反三角函数与最简三角方程
反正弦 |x ≤1,arcsinx∈[-π/2,π/2],sin(arcsinx)=x,
反余弦 |x ≤1,arccosx∈[0,π],cos(arccosx)=x.
反正切 x∈R,arctanx∈(-π/2,π/2),tan(arctanx)=x.
方程 sinx=a,|a ≤1,则 x=2kπ+arcsina,或x=2kπ+π-arcsina,(k∈Z)
方程 cosx=a,|a ≤1,则 x=2kπ±arccosx,(k∈Z)
方程 tanx=a,a∈R,则 x=kπ+arctana,(k∈Z)
(3)加法定理与解斜三角形
|
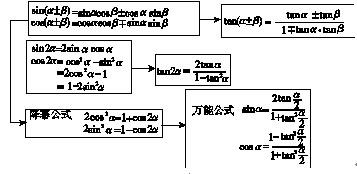
(4)斜三角形的边角关系与面积
|
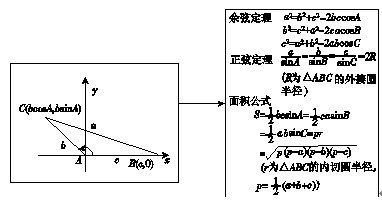
5.向量
|
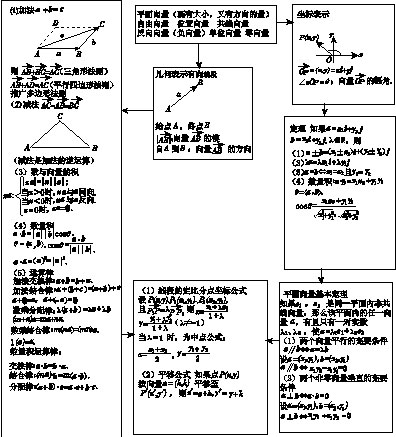
6.直线和圆
|
基本公式
|
|
|
两点间
的距离
|
|AB =
|
|
线段的定比
分点公式
|
x=''y=
|
|
线段的中点
坐标公式
|
x=''y=
|
|
直线方程
|
|
|
斜截式
|
y=kx+b
|
|
点斜式
|
y-y1=k(x-x1)
|
|
两点式
|
(y-y1)(x2-x1)=(x-x1)(y2-y1)
|
|
截距式
|
+=1
|
|
参数式
|
α为直线的倾角,t=P0P
|
|
直线Ax+By+C=0(A2+B2≠0)的方向向量为(B,-A);法向量为(A,B)
|
|
点P0(x0,y0)到直线Ax+By+C=0(A2+B2≠0)的距离:
d=|Ax0+By0+C/√A2+B2
两直线的交角:
l1到l2所成的角φ(l1、l2的斜率分别为k1、k2),tanφ=k2-k1/1+k1k2
l1到l2的夹角(不大于直角)φ0,tanφ0=| k2-k1/1+k1k2
对称问题(均归结为点关于对称中心、对称轴的对称)
|
已知点
|
对称中心或对称轴
|
对称点
|
|
P(a,b)
|
|
|
|
点(0,0)
|
P′(-a,-b)
|
|
|
点(m,n)
|
P′(2m-a,2n-b)
|
|
|
直线 x=m
|
P′(2m-a,b)
|
|
|
'''x=0
|
P′(-a,b)
|
|
|
直线 y=n
|
P′(a,2n-b)
|
|
|
'''y=0
|
P′(a,-b)
|
|
|
直线 y=x
|
P′(b,a)
|
|
|
'''y=-x
|
P′(-b,-a)
|
|
当对称轴为Ax+By+C=0(A2+B2≠0),点(a,b)的对称点
P′(x0,y0)满足{y0-b/xo-a(-A/B)=-1.Axo+a/2+By0+b/2+C=0}
圆
圆的标准方程:(x-x0)2+(y-y0)2=r2,圆心:(x0,y0),半径:r
原点为圆心、半径为r的圆的方程:x2+y2=r2
圆的参数方程:{x=ycosθ.y=rsinθ}
圆的一般方程:x2+y2+Dx+Ey+F=0
D2+E2-4F>0,实圆,半径:
''圆心:(-D/2,-E/2)
D2+E2-4F=0,点圆,即:(-D/2,-E/2)
D2+E2-4F<0,虚圆(无轨迹)
直线lx+my+n=0与圆(x-x0)2+(y-y0)2=r2的位置关系:
<r⇔相交 =r⇔相切
>r⇔相离
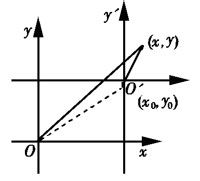
平移变换
坐标轴平移变换方程:{X=X'+X0.Y=Y'+Y0} 其中(x0,y0)为新原点O′的坐标
|
7.不等式
|
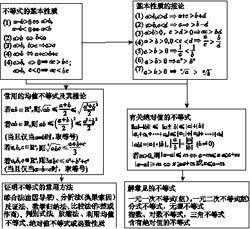
一元二次不等式
一元二次方程ax2+bx+c=0(a≠0)'判别式Δ=b2-4ac.
Δ>0, 两根为x1=,x2=;
Δ=0,'两根为x1=x2=-b/2a.
Δ<0,'有两共轭虚根(无实根)
一元二次不等式的解集:记ax2+bx+c=f(x).
|
|
Δ>0
|
Δ=0
|
Δ<0
|
|
f(x)>0,a>0
|
(-∞,x1)∪(x2+∞)
|
(-∞,-)∪(-,+∞)
|
(-∞,+∞)
|
|
f(x)<0,a>0
|
(x1,x2)
|
|
|
分式不等式 >0⇔(ax+b)(cx+d)>0
无理不等式 >a⇔
≤a⇔
对于有理不等式,还可以应用标根法。
8.圆锥曲线
| |
椭圆
|
双曲线
|
抛物线
|
|
|
|
| |
|
|
|
|
|
|
|
定义1
|
集合
{M MF1|+|MF2|=2a,
'2a>|F1F2|}
定点F1、F2叫椭圆的焦点
|
集合
{M MF1|-|MF2|=2a,
'0<2a<|F1F2|}
定点F1、F2叫双曲线的焦点
|
|
|
|
|
|
定义2
|
集合
{M =e,0<e<1}
F为焦点,d为点M到相应准线l的距离
|
集合
{M =e,e>1}
F为焦点,d为点M到相应准线l的距离
|
点集{M =e=1}
F为焦点,d为点M到准线l的距离
|
|
|
|
|
图形
|
DS11.TIF
|
BP]
|
DS12.TIF
|
BP]
|
DS13.TIF
|
BP]
|
|
标准方程
|
+=1(a>b>0)
长轴长 |A1A2|=2a
短轴长 |B1B2|=2b
|
-=1(a>0,b>0)
实轴长 |A1A2|=2a
虚轴长 |B1B2|=2b
|
y2=2px(p>0)
p为焦点到准线l的
距离
|
|
|
|
|
参数方程
|
(φ为参数)
|
(θ为参数)
|
(t=cotφ为参数)
|
|
|
|
|
顶点
|
(-a,0),(a,0)
(0,-b),(0,b)
|
A1(-a,0),A2(a,0)
|
O(0,0)
|
|
|
|
|
焦点
|
F1(-c,0),F2(c,0)
焦距|F1F2|=2c
c2=a2-b2
|
F1(-c,0),F2(c,0)
焦距|F1F2|=2c
c2=a2+b2
|
F(,0)
|
|
|
|
|
离心率
|
e=(0<e<1)
|
e=(e>1)
|
e=1
|
|
|
|
|
准线
|
l1:x=-,l2:x=
|
l′:x=-,l:x=
渐近线为y=±x
|
x=-
|
|
|
|
|
0对称轴
|
x=0,y=0
|
x=0,y=0
|
y=0
|
|
|
|
|
焦半径
|
|PF1|=e,|PE′|=a+ex
PF2|=e,|PE =a-ex
|
当x≥a时,
PF1|=ex+a,
PF2|=ex-a
当x≤-a时,
PF1|=-(ex+a),
PF2|=-(ex-a)
|
|PF =x+
|
|
|
|
|
通径
|
|HH′|=
|
|HH′|=
|
|HH′|=2p
|
|
|
|
|
辅助圆
|
x2+y2=a2(大),
x2+y2=b2(小)
|
x2+y2=a2,x2+y2=b2
|
|
|
|
|
|
上一页
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
下一页
|
<< 上一页 [11] [12] [13] [14] [15] [16] 下一页

