第三章 知识大盘点
高考数学知识网络图:
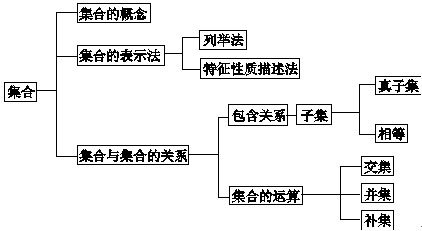
1.集合与常用逻辑用语
| |
|

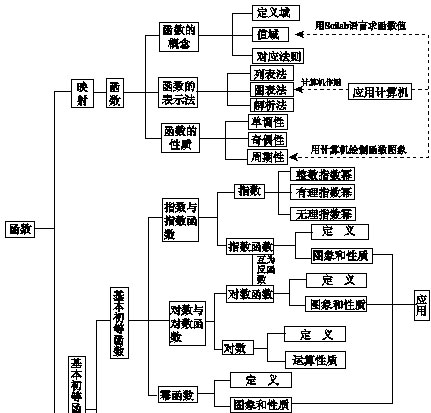
2.函数及基本初等函数(Ⅰ)
|
|
(1)
(2)指数函数图象和性质
|
a
|
a>1
|
0<a<1
|
|
y=ax
|
|
|
|
定义域
|
R
|
R
|
|
值域
|
x≥0时,y≥1
x<0时,0<y<1
|
x≥0时,0<y≤1
x<0时,y>1
|
|
定点
|
过点(0,1)
|
过点(0,1)
|
|
单调性
|
单调递增
|
单调递减
|
(3)对数函数图象和性质
|
a
|
a>1
|
0<a<1
|
|
性质
|
|
|
|
①定义域:(0,+∞)
|
|
|
|
②值域:R
|
|
|
|
③过点(1,0),即当x=1时,y=0
|
|
|
|
④在(0,+∞)上是增函数
|
在(0,+∞)上是减函数
|
|
|
⑤x>1时,y>0;0<x<1时,y<0
|
x>1时,y<0;0<x<1时,y>0
|
|
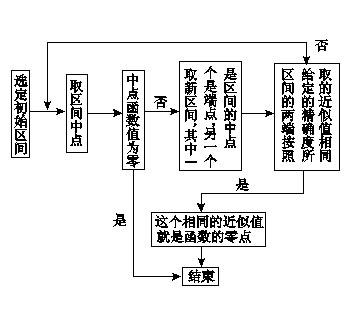
(4)函数有零点的判定
如果函数y=f(x)在一个区间[a,b]上的图象不间断,并且在它的两个端点处的函数值异号,即f(a)·f(b)<0,则这个函数在这个区间上,至少有一个零点,即存在一点x0∈(a,b),使f(x0)=0,这样的零点叫做变号零点,有时曲线通过零点时不变号,这样的零点叫做不变号零点。
函数的零点、方程的根、函数图象与x轴的交点的横坐标,实质是同一个问题的三种不同表现形式,如方程根的个数就是函数零点的个数,也就是函数图象与x轴的交点个数。
用计算机操作求零点近似值,其操作步骤如图所示:
|
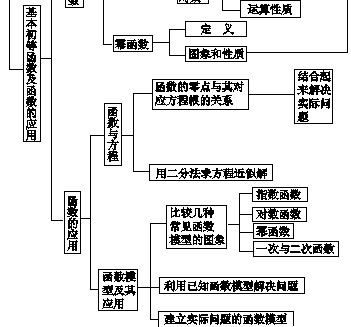
(5)常见的几种函数模型
①一次函数型y=kx+b;
②反比例函数型y=k/x(k≠0);
③二次函数型y=ax2+bx+c(a≠0);
④指数函数型y=N(1+p)x(增长率问题)(x>0);
⑤y=x+a/x型;
⑥分段函数型。
3.立体几何初步
(1)
|
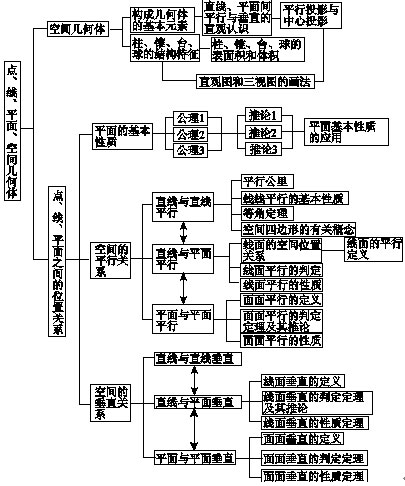
(2)
凸多面体 棱柱 直棱柱 正棱柱
|
性质
|
|
1.平行于底面的截面是与上、下底面全等的正多边形
2.过不相邻的两条侧棱的截面是矩形
|
|
性质
|
|
1.平行于底面的截面是与底面相似的正多边形
2.过不相邻的两条侧棱的截面是等腰梯形
3.侧面是全等的等腰梯形
|
|
度量
|
|
S棱台侧=(c1+c2)h′
V棱台=(S1+S2+)h
|
(c1、c2为上下底周长,h′为斜高,S1S2为上下底面积,h为高)棱锥 正棱锥
|
性质
|
|
1.平行底面的截面是与底面相似的正多边形
2.过不相邻的两条侧棱的截面是等腰三角形
3.侧面是相互全等的等腰三角形
|
(以上体积公式对一般棱锥台均适用)
|
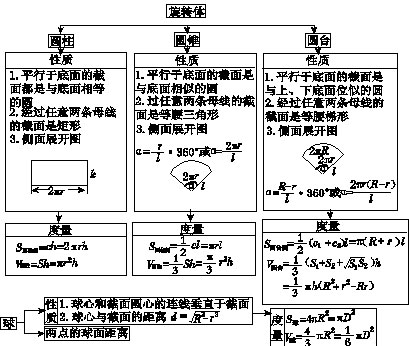
注:球面距离(球面上经过两点的大圆在这两点间的一段劣弧的长度),计算A、B两点间的球面距离关键是搞清纬度、经度、经度差、纬度差等概念,求球面上两点A、B间的距离的步骤:①计算线段AB的长;②计算球心角AOB的弧度数;③用弧长公式计算劣弧AB的长。
|

(3)
(上面符号“(l)α=a”表示“直线l在平面α上的射影为a”)
(4)
|
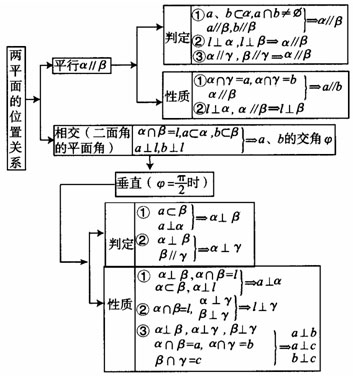
(5)三视图:选取三个两两垂直的平面作为投射面,一个水平放置,叫做水平投射面,投射到这个平面内的图形叫做俯视图;一个投射面放置在正前方,这个投射面叫做直立投射面,投射到这个平面内的图形叫做主视图;和直立、水平两个投射面都垂直的投射面叫做侧立投射面,通常把这个平面放在直立投影面的右面,投射到这个平面内的图形叫做左视图。将空间图形向这三个平面作正投影,然后把这三个投影按一定的布局放在一个平面内,这样构成的图形叫做空间图形的三视图。
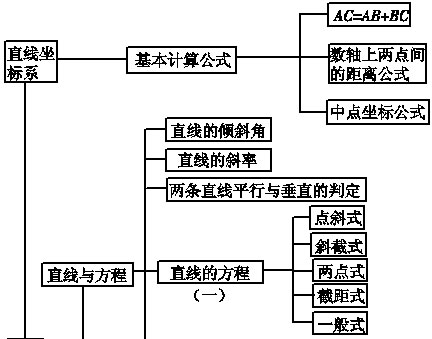
4.平面解析几何初步
|
|
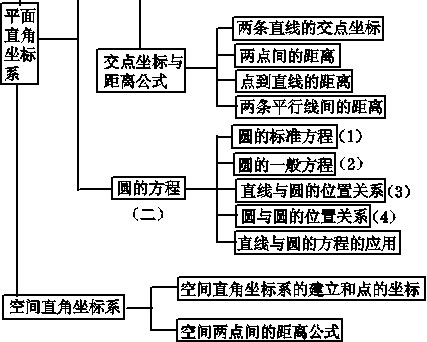
(1)直线方程的五种形式
①点斜式:已知直线过点(x0,y0),斜率为k,则直线方程为y-y0=k(x-x0),它不包括垂直于x轴的直线;②斜截式:已知直线在y轴上的截距为b,斜率为k,则直线方程为y=kx+b,它不包括垂直于x轴的直线;③两点式:已知直线经过P1(x1,y1),P2(x2,y2)两点,则直线方程为x-x1/x2-x1=y-y1/y2-y1,它不包括垂直于坐标轴的直线;④截距式:已知直线在x轴和y轴上的截距为a,b,则直线方程为x/a+y/b=1,它不包括垂直于坐标轴的直线和过原点的直线;⑤一般式:任何直线均可写成Ax+By+C=0(A,B不同时为0)的形式。
注:求直线方程的基本思想和方法是恰当选择方程的形式,利用待定系数法求解。
(2)①圆的标准方程
圆心为(a,b),半径为r的圆的标准方程为(x-a)2+(y-b)2=r2.说明:方程中有三个参量a、b、r,因此三个独立条件可以确定一个圆。
②圆的一般方程
二次方程x2+y2+Dx+Ey+F=0(*),将(*)式配方得(x+D/2)2+(y+E/2)2=D*D+E*E-4F/4.
当D2+E2-4F>0时,方程(*)表示圆心(-D/2,-E/2),半径r=1/2√D*D+E*E-4F的圆,把方程x2+y2+Dx+Ey+F=0(D2+E2-4F>0)叫做圆的一般方程。
说明:Ⅰ.圆的一般方程体现了圆方程的代数特点:a.x2、y2项系数相等且不为零.b.没有xy项。
Ⅱ.当D2+E2-4F=0时,方程(*)表示点(-D/2,-E/2),当D2+E2-4F<0时,方程(*)不表示任何图形。
Ⅲ.据条件列出关于D、E、F的三元一次方程组,可确定圆的一般方程。
③研究直线与圆的位置关系有两种方法:一是将直线与圆的交点问题转化为研究它们的方程所组成的方程组有几个实数解的问题。通常利用判别式法。若Δ>0有2解,则直线与圆相交;若Δ=0有1解,则直线与圆相切;若Δ<0,无解,则直线与圆相离。二是将直线与圆的位置关系转化为判定圆心到直线的距离d与半径r大小的比较。若d>r,直线与圆相离;若d=r,直线与圆相切;若d<r,则直线与圆相交。解析几何通常使用第2种方法。
④判定两圆的位置关系的方法有二:第一种是代数法,研究两圆的方程所组成的方程组的解的个数;第二种是研究两圆的圆心距与两圆半径之间的关系。第一种方法因涉及两个二元二次方程组成的方程组,其解法一般较烦琐,故使用较少,通常使用第二种方法,具体如下:
圆(x-a1)2+(y-b1)2=r与圆(x-a2)2+(y-b2)2=r的位置关系,其中r1>0,r2>0.
设两圆的圆心距为d,则
d=√(a1-a2)(a1-a2)+(b1-b2)(b1-b2),
当d>r1+r2时,两圆外离;
当d=r1+r2时,两圆外切;
当|r1-r2|<d<|r1+r2|时,两圆相交;
当d=|r1-r2|时,两圆内切;
当0<d<|r1-r2|时,两圆内含。
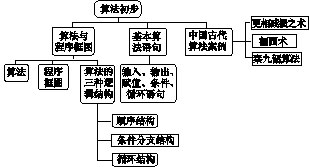
5.算法
|
上一页 [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] ... 下一页 >>

