8.基本初等函数(Ⅱ)及三角恒等变换
| |
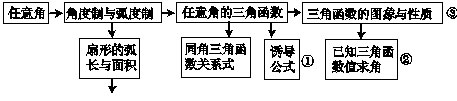
同角三角函数关系式:
(1)平方关系:sin2α+cos2α=1,1+tan2α=sec2α,1+cot2α=csc2α;
(2)倒数关系:sinαcscα=1,cosαsecα=1,tanαcotα=1;
(3)商数关系:tanα=sinα/cosα,cotα=cosα/sinα.
①诱导公式的规律可简记为:奇变偶不变,符号看象限。此外在应用时,不论α取什么值,我们始终视α为锐角。否则,将导致错误。诱导公式的应用是求任意角的三角函数值,其一般步骤:a.负角变正角,再写成2kπ+α,0≤α<2π;b.转化为锐角。
②求角的方法:先确定角的范围,再求出关于此角的某一个三角函数(要注意选择,其标准有二:一是此三角函数在角的范围内具有单调性;二是根据条件易求出此三角函数值).
③三角函数的图象与性质:
|
三角函数
|
y=sinx
|
y=cosx
|
y=tanx
|
y=cotx
|
|
定义域
|
(-∞,+∞)
|
(-∞,+∞)
|
(nπ-,nπ+)
|
(nπ,nπ+π)
|
|
值域
|
[-1,1]
|
[-1,1]
|
(-∞,+∞)
|
(-∞,+∞)
|
|
最大(小)
值(k∈Z)
|
当x=2kπ+
时,ymax=1;
当x=2kπ-
时,ymin=-1
|
当x=2kπ时,
ymax=-1;
当x=2kπ+π
时,ymin=-1
|
无
|
无
|
|
奇偶性
|
奇函数
|
偶函数
|
奇函数
|
奇函数
|
|
周期性
|
T=2π
|
T=2π
|
T=π
|
T=π
|
|
有界性
|
有界
|
有界
|
无界
|
无界
|
|
单调性
(k∈Z)
|
在[2kπ-,
2kπ+]
上都是增函数,
在[2kπ+,
2kπ+]
上都是减函数
|
在[(2k-1)π,2kπ]
上都是增函数,
在[2kπ,(2k+1)π]
上都是减函数
|
在(kπ-,
kπ+)
内都是增函数
|
在(kπ,kπ+π)
内都是减函数
|
|
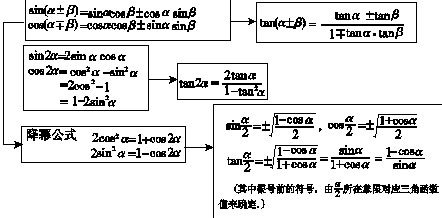
(ⅰ)公式间的关系
相除相除相除
(ⅱ)辅助角公式:asinα+bcosα=√a*a+b*bsin(α+φ)(辅助角φ所在象限由点(a,b)的象限决定,tanφ=b/a).
(ⅲ)三角函数的化简、计算、证明的恒等变形的基本思路是:一角二名三结构。即首先观察角与角之间的关系,注意角的一些常用变式,角的变换是三角函数变换的核心;第二看函数名称之间的关系,通常“切化弦”;第三观察代数式的结构特点。基本的技巧有:
a.巧变角(已知角与特殊角的变换、已知角与目标角的变换、角与其倍角的变换、两角与其和差角的变换。如α=(α+β)-β=(α-β)+β,2α=(α+β)+(α-β),2α=(β+α)-(β-α),α+β=2·α+β/2,α+β/2=α-β/2-α/2-β等).
b.三角函数名互化(切割化弦).
c.公式变形使用如:tanα±tanβ=tan(α+β)(1∓tanαtanβ).
d.三角函数次数的降升(降幂公式:cos2α=1+cos2α/2,sin2α=1-cos2α/2;升幂公式:1+cos2α=2cos2α,1-cos2α=2sin2α).
e.式子结构的转化(对角、函数名、式子结构化同).
f.常值变换主要指“1”的变换(1=sin2x+cos2x=sec2x-tan2x=tanxcotx=tanπ/4=sinπ/2=…).
上一页 [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] ... 下一页 >>

