知识概述

　　在计数时，必须注意无一重复，无一遗漏。为了使重叠部分不被重复计算，人们研究出一种新的计数方法，这种方法的基本思想是：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理。

　　容斥问题也是行政职业能力测验考试中数学运算部分常考题型之一。

　　“容斥原理”问题的难点在于：1、读懂题目难；2、明白各部分间包含关系难；3、计算易出错。解决这类问题一般使用下面两种方法。

　　一、容斥原理公式法：适用于题目条件与问题都可直接代入公式的题目。核心公式如下：

　　两个集合的容斥关系公式：A∪B = A+B-A∩B (∩:重合的部分)

　　三个集合的容斥关系公式：A∪B∪C=A+B+C-A∩B-B∩C-C∩A +A∩B∩C

　　二、文氏图示意法：用图形来表示集合关系，更加直观。

　　典例分析

　　例1：一个停车场有50辆汽车，其中红色轿车35辆，夏利轿车28辆，有8辆既不是红色轿车又不是夏利轿车，问停车场有红色夏利轿车多少辆？(    )

　　A. 14               B. 21               C. 15               D. 22

　　京佳解析：B    两集合容斥原理。设全集Q表示停车场一共有50辆汽车，集合A表示红色车数量，B表示夏利车数量。有题目我们已知A等于35。B等于28。由已知非A非B的数量是8，也即Q－A∪B＝8。所求的是红色夏利车辆数，既是求A∩B的值。设所求为x，根据容斥原理公式有：35＋28－x50－8＝35＋28－x，计算得到x＝21。故选B。

　　例2：一学校的750名学生或上历史课，或上算术课，或两门课都上。如果有489名学生上历史课，606名学生上算术课，问有多少学生两门课都上？( 　)

　　A. 117　　      B. 144　　　　　  C. 261　　　      D. 345

　　京佳解析：D    两集合容斥问题。根据题目已知条件和容斥原理公式知，两门都上的有489＋606－750＝345人。故选D。

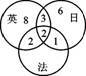
　　例3：外语学校有英语、法语、日语教师共27人，其中只能教英语的有8人，只能教日语的有6人，能教英、日语的有5人，能教法、日语的有3人，能教英、法语的有4人，三种都能教的有2人，则只能教法语的有( 　)。

　　A.4人             B.5人            C.6人              D.7人

　　京佳解析：B    三集合容斥。此题应用文氏图法，将能教英语、日语、法语的教师分别设为不同的集合。先设所有集合的交集为2，依题意得文氏图(见右图)，由图知：只能教法语的老师为：27－8－6－3－2－2－1＝5人。

　　例4：对厦门大学(微博)计算机系100名学生进行调查，结果发现他们喜欢看NBA和足球、赛车。其中58人喜欢看NBA；38人喜欢看赛车，52人喜欢看足球，既喜欢看NBA又喜欢看赛车的有18人，既喜欢看足球又喜欢看赛车的有16人，三种都喜欢看的有12人，则只喜欢看足球的有(    )。

　　A.22人             B.28人             C.30人             D. 36人

　　京佳解析：A    三集合容斥。总人数减去喜欢NBA的和喜欢赛车的，再加上既喜欢NBA又喜欢赛车的，就得到只喜欢足球的。100－58－38＋18＝22。